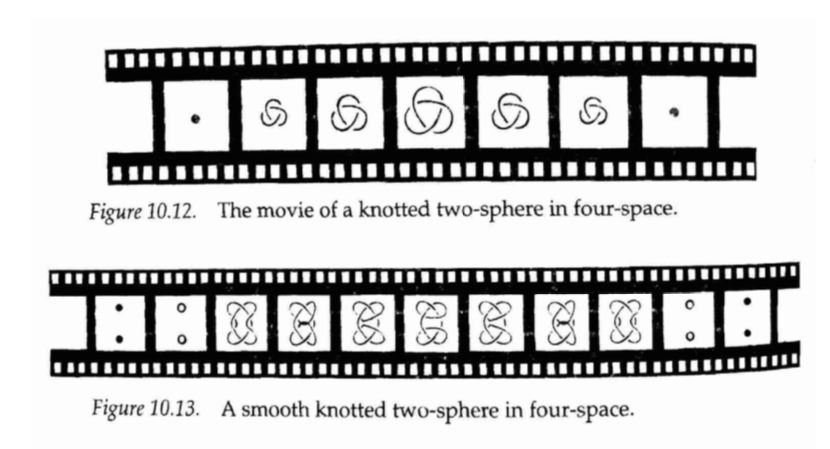
Knots are 1-dimensional objects embedded in 3-dimensional space. So generalizing in an n-dimensional space, a knot would be an embedded (n-2)-dimensional object. Therefore in a 4-dimensional space we would embed a (4-2)-dimensional object, or a 2-dimensional object. Now when trying to visualize a 2-dimensional knot we need to come up with a fourth dimension. This extra dimension needs to be some continuous aspect which we can measure across a spectrum.
One possibility for a fourth dimension is time. With time as the fourth dimension, imagine a two dimensional object, S^2 or surface, the sphere knotted in four dimensions. One possible method of visualizing such an object is imagining a discrete sequence of slides depicting one dimensional knots over time (the 2nd dimension of the knot). So each slide would be a different cross-section of the whole 2-dimensional knot. The knotted sphere represented would connect each cross section. The two dimensional analog to the unknot would be the sphere. And just as every one dimensional knot is homeomorphic to a circle, every two dimensional knot is homeomorphic is a sphere. Each figure below depicts the cross-sections of a 2-dimensional knot.
Another possibility for a fourth dimension is color. Let the second dimension on the knot be color. Then instead of a sphere, the 2-dimensional knot is circle which can be colored any shade. Strands of different colors would be allowed to pass through each other because they are considered different ’planes’ in the color-dimension. Therefore by adjusting the shade of the appropriate strands, every knot could be reduced to the unknot. So to make the study of two dimensional knots meaningful, changing the shade of a strand would change the knot classification. This is analogous to distinguishing between homeomorphisms and ambient isotopies for one dimensional knots.
It is possible to imagine ever higher dimensional knots by combining even more dimensions, such as both color and time in the same space. Higher dimensional knots are connected with other sub disciplines of mathematics, including but not limited to algebraic topology and surgery theory.