Knot so humble beginnings
Knot Theory is a relatively new field of mathematics, and an active realm of contemporary research. It all began from a misconception in the early 1800s. Lord Kelvin theorized that different types of matter corresponded with different knots of ether. Ether was theorized to be a substance which pervaded all space and allowed the transmission of gravitational and electromagnetic forces, analogous to sound waves in the air. This idea inspired physicists, chemists, and mathematicians alike to begin analyzing the structure of knots and cataloging unique knots. Then in 1887 the Michelson-Morley Experiment, and subsequent experiments of similar nature, debunked the existence of a substance resembling ether [1]. This revelation removed the real-world application of Knot Theory and lead to applied scientists largely forgoing work on knots. However the newly formed theory was adopted and nurtured by pure mathematicians for the next century.
Coming full circle, in the 1980s chemists observed knotting in the double helix structure of DNA molecules. They also developed the technology to create their own knotted molecules in which the knotting of the molecule would affect its properties. Another active avenue of study is to discover the ideal representation of a knot by analyzing the potential energy [2]. For the last few decades applied scientists have once again been contributing to the field of Knot Theory.
What are Knots?
A mathematical knot is somewhat similar to the everyday definition as it can constructed from tangles of string or rope. However, a mathematical knot cannot be untied. It is an embedding of a circle in 3-dimensional space. In other words if you took a string and looped it around itself to create overlaps and then glued the two ends together, you would have a representation of a mathematical knot. Once the ends are glued together a mathematical knot cannot be changed without ripping or cutting the string itself. Also because knots fall under the purview of Topology, distance (measure) does not matter when differentiating between knots. What does matter when differentiating between knots is how the knot sits in the space.
Examples of Knots
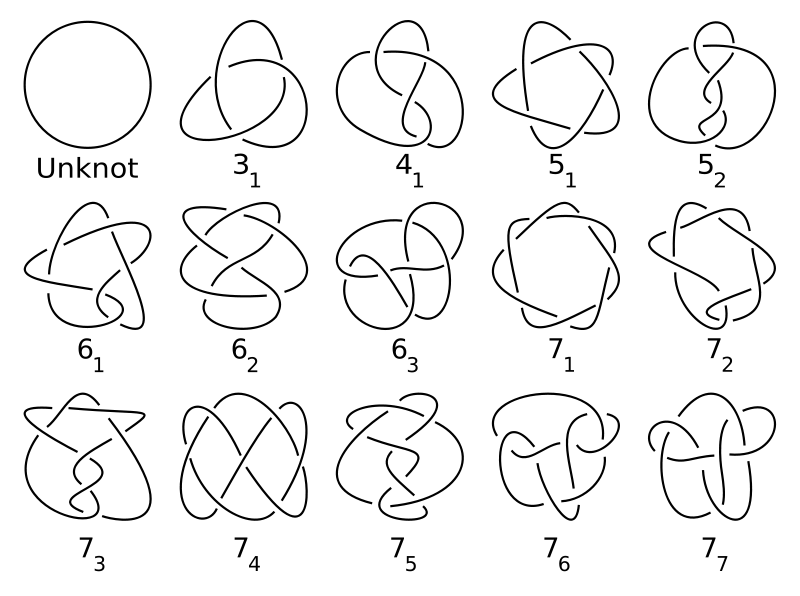
It is important to note that each diagram is not unique; there are many different diagrams which represent the same knot.
Challenge: Some, but not all of the 3-dimensional knots have 2-dimensional matches in the table below. Can you find the matches?
Mathematical Definition: A knot is a subset of R3 that is homeomorphic to the circle S1, a closed, non-self-intersecting curve that is embedded in three dimensions and cannot be untangled to produce a simple loop.
Let’s take apart the definition piece-by-piece. We start with a basic circle. This is a 1-dimensional object because a mathematical circle has no width, it is simply a line curved back onto itself. Closed means there are no gaps or holes in the line of the circle. And non-intersecting means the line does not run into itself anywhere.
We take this naturally 1-dimensional circle and place it in 3 dimensions. This allows the circle 2 more dimensions of freedom to ‘knot’, or curve around itself before closing the circle.
[1] Colin C. Adams. The Knot Book. American Mathematical Society, 2001.
[2] Louis H. Kauffman. Knots and physics. 66:46–67, 2008.